estimates - E-number of magic hypercubes

Estimates of the number of magic squares, cubes, ... (hypercubes)

E-Number of a magic hypercube

Dimension: n Order: m

with u_m = mⁿ - (m - 1)ⁿ - 1 + 2^n-1 and N_n(m) = Number of magic series.

What improvements of the simple concept on the previous page are neccessary?
- How many 'regular number hypercubes' do exist?
- How many aspects does a hypercube of dimension n posses?
- What is the probability of the first magic line?
- How many unforced magic lines are there?

Define a normal number hypercube of dimension n and order m as a mⁿ-array of positive integers from 1 to mⁿ.
There are mⁿ! ways to arrange the mⁿ numbers. Therefore we get

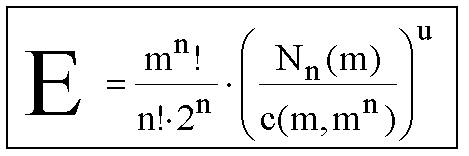
W = mⁿ!

normal number hypercubes

Aspects
The number A of aspects of a hypercube depends on its dimension n but not on its order m.
a) There are 2ⁿ ways to combine reflections of a hypercube in the direction of any axis.
This can also be considered as inverting the order of certain coordinates.
b) Other aspects can be achieved by interchanging coordinates:
As we got n coordinates, there are n! permutations of them.
Thus we get the following formula for the number of aspects:

A = n! · 2ⁿ

aspects of hypercubes

Magic probability
There are N_n(m) magic series of dimension n and order m.
And there are c(m, mⁿ) combinations of m numbers selected from mⁿ numbers.
Thus the exact probability of magicness for a random line with m numbers and no further constraints is:

p = N_n(m) / c(m, mⁿ)

probability of the first magic line

Unforced magic lines
Again we assume the same probability p for other lines to be magic if they are not forced to be magic.
The number u of unforced magic lines depends on the dimension, the order and the magic properties of the hypercube.
Consider a random number cube of order m and begin to check the rows on magicness. Only one of the m² rows is forced to be magic. Now check the columns: already the n^th column is forced to be magic. Because m rows and m columns form a semi-magic sub-square of the cube. That is the same in the other planes. From m pillars there is one forced to be magic for the first (m-1) planes which they build with rows. In the last plane every pillar is forced to be magic (consider planes formed by pillars and columns).
That makes u = m² - 1 + m · (m - 1) + (m - 1)² unforced magic lines of an order-m semi-magic cube.
And u = m^n-1 - 1 + m^n-2 · (m - 1)¹ + m^n-3 · (m - 1)² + ... + (m - 1)^n-1 unforced magic lines in a semi-magic hypercube.
This formula can be written in a perplexing simple way:

u_sm = mⁿ - (m - 1)ⁿ - 1

unforced magic lines in a semi-magic hypercube.

In a regular magic hypercube the longest diagonals (the so-called n-agonals) have to be magic. As these lines connect two opposite corners there are half as much n-agonals than corners of the hypercube.

u_m = mⁿ - (m - 1)ⁿ - 1 + 2^n-1

unforced magic lines in a regular magic hypercube.

Definition
Consider a regular number hypercube of order m and dimension n with certain magic properties (semi-magic or normal magic or pandiagonal magic or ...) and u unforced magic lines then the E-number (estimate number) of this hypercube is defined by the following equation:

E = mⁿ! · p^u / A

with

p = N_n(m) / c(m, mⁿ)

and

A = n! · 2ⁿ

- N_n(m) is the number of magic series of dimension n and order m. See magic series!
- c(m, mⁿ) is the number of combinations of m numbers selected from mⁿ ones.
- A is the number of aspects that a hypercube has got in dimension n.
- u is the number of unforced magic lines. See chapter above.

Back to the Table of Contents