estimates - E-number

Estimates of the number of magic squares, cubes, ... (hypercubes)

The E-Number

Abstract
The E-number is defined exactly. It enables us to estimate the numbers of magic squares, cubes, ...
For magic objects with symmetric structures this statistical method fails without further adaptions.
For an easier description of the matter I mainly use order m = 5 as example.
But all can be done for any other order m > 1 as well.

Normal number squares
Imagine a 5x5-array of positive integers from 1 to 5² = 25.
There are 25! = 25·24·23· ... ·3·2·1 ways to arrange the 25 numbers.
Such an array is called a normal number square of order 5.

Magic probability
Remember that the magic constant of an order-5 magic square is S = (5² + 1)·5 / 2 = 65.
Consider the first row of a random order-5 normal number square.
Say p is the probability that the 5 numbers in this row sum up to the magic constant 65.
p may be called magic probability of a normal magic order-5 square.

There are c(5, 25) = 53130 combinations of 5 numbers selected from 25 numbers.
- Formula: c(5, 25) = 25! / (20!·5!) = 25·24·23·22·21 / 5·4·3·2·1

And there are N₂(5) = 1394 combinations with the sum 65.
- These combinations are called magic series of order 5.

Magic probability p = N₂(5) / c(5, 25) = 1394 / 53130 ≈ 0.0262375

Next rows
What about the second row?
What is the conditional probability p_r2 that row 2 is magic too?
It is a little greater than p.
But we don't mind and write approximately: p_r2 ≈ p.
Go on with p_r3 ≈ p and p_r4 ≈ p.

Order 5 is the greatest order where we are able to determine these conditional probabilies exactly.
This was first done by the Frenchman Francis Gaspalou in 2005.
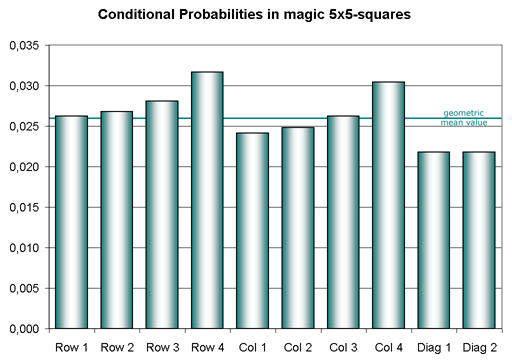
The diagram also shows the probabilities of columns and diagonals, calculated 2005-11-24.
The coloured horizontal line shows the geometric mean value p_mean of the 10 probabilities.

Click on the diagram in order to enlarge it.

Last row
Why don't we claim p_r5 ≈ p ? Because p_r5 = 1.
This is also true for the last column: p_c5 = 1.
If 4 rows (columns) are magic then the 5^th, the last one is magic too.
Proof: The sum of all numbers from 1 to 25 equals 5 · 65 and each of the four first rows (columns) has the sum 65.

Columns and diagonals
We also estimate the conditional probabilities p_c1, ..., p_d2 for columns (without the last one) and diagonals by p.
Choose a random normal number square. What is the (total) probability p_total that this square is a magic square?
Exact value: p_total = p · p_r2 · p_r3 · p_r4 · p_c1 · p_c2 · p_c3 · p_c4 · p_d1 · p_d2 = p_mean¹⁰
Estimate: p_total ≈ p¹⁰

Why don't we use p_mean instead of p = p_r1 ?
Because we can't calculate p_mean for orders greater than 5. But we can calculate p exactly up to order 54 and have got very good approximations for higher orders.

Number of unforced magic lines u
In a magic square the last row and the last column are forced to be magic (p_r5 = 1 and p_c5 = 1).
The conditional probability to be magic is smaller than 1 for the other rows, the other columns and the diagonals.
Say u is the number of these 'unforced magic lines'. For an order-5 magic square: u = 10.
A mathematician would say u is the rank of the equations system of a magic square.

Definition
If number squares of order m have certain magic properties (semi-magic or normal magic or pandiagonal magic or ...) with u unforced magic lines then the E-number (estimate number) for these squares is defined by the following equation:

E = m²! · p^u / 8

with

p = N₂(m) / c(m, m²)

- N₂(m) is the number of magic series of order m (and dimension 2). See magic series!
- c(m, m²) is the number of combinations of m numbers selected from m² ones.
- We have to devide by 8 because it is usual to count only one aspect of each square.
You get other aspects by rotating or reflecting the square. All in all there are A = 8 aspects of a square.

What is the E-number for normal magic squares of order 5?
Unforced magic lines: 4 rows, 4 columns, 2 diagonals → u = 10
E = 5²! · p¹⁰ / 8 with p = 1394 / 53130
E = 299 768 000
Of course we can't expect that this is exactly the number of magic order-5 squares.
This number was first determined by Richard Schroeppel (USA):
N = 275 305 224
The relative aberration of E is about 9% here. Not too bad for a rather simple estimate.

Back to the Table of Contents