Voderberg Nonagons

How to construct a Voderberg nonagon

Step 0
First choose an angle ε for the nose of the tile. In order to be able to build spirals with the tile, there has to exist an integer k with k·ε=180°. The most suitable integer values for ε are 12°, 15°, and 18°. But also ε=180°/11 makes sense. A construction with ε≥180°/7 is not possible because for ε>23.90571178140393° the red circle and the blue line in step 3 do not intersect. See appendix 3. This restriction is not valid for VT-tiles with more than 9 edges.

Step 1
Start the construction with the 5 points Z, R, S, T and U. RSZ is an isosceles triangle with angle ε at the apex Z. The straight line segment TZ is twice as long as RS. TZ and RS are parallel. The triangle TUZ is also isosceles with angle ε at the apex Z. There are many different ways to construct these 5 points with ruler and compass. We suggest to use an interactive geometry software like GeoGebra.
But you also can calculate the coordinates of the points. For no good reason we use 2 units for the distance of R and S. Then the distance of T and Z is 4 units. We suggest the following coordinates: Z(0, 0) and T(-4, 0).
Then we have U(-4cos ε, -4sin ε), R(-1, -w) and S(1, -w) with w = cot(ε/2).
Z, T and U are vertices of the Voderberg nonagon, whereas R and S are necessary for the construction, they lay on edges of the nonagon, but are not vertices of the tile.

Step 2
We obtain V by reflecting T at R and W by reflecting U at S.
The coordinates: V(2, -2w) and W(2 + 4cos ε, -2w - 4sin ε). Don't draw the orange lines.
Note that a rotation around Z by the angle ε moves T on U, R on S and V on W.

Step 3
Choose a point A inside the green area between the red circle with center M and left from the ray TU (blue line). If A would lay on the blue ray we would not obtain a nonagon because U would be an element TA. If A would lay on the red circle the point B (constructed in the next step) would be an element of AR.
The center M of the circle is the intersection of the perpendicular from R on TZ and the perpendicular bisector of the points R and Z.
It is also possible to choose A without constructing the red circle because the next step will show whether your choice was suitable.

Step 4
Constructing the vertices B, C and D:
B is obtained by rotating A around Z with angle ε (counterclockwise).
C is the reflection of A at R.
D is the reflection of B at S.
ZTACVWDBU is a Voderberg nonagon.

Up to translation, rotation, reflection and homothety a Voderberg nonagon is given by the position of Point A relative to the points Z and T.

The surrounding and periodical tiling properties of the Voderberg nonagon are possible because of three facts.
We do not consider the non-periodic rotational and spiral tilings here.

Fact 1: We obtain the red path ZUBDW (right side) by rotating the blue path ZTACV (left side) around Z with angle ε.
This allows us to paste the left side of a copy (yellow) of the nonagon exactly at the red path (right side) of the original nonagon.

Fact 2: The violet path ZUBDWV is point symmetric with respect to the point S.
This allows us to paste a 180° rotated copy (yellow) of the nonagon exacty at the violet path of the original nonagon (cyan).

Fact 3: The patch of two tiles shown in in Fact 2 is an octagon that is point symmetric with respect to the point S. Therefore Z'T' and TZ have same length and orientation. The same is true for C'A' and AC, ZC' and CZ' as well as A'T' and TA. As TACZ' is point symmetric with respect to R line segment CZ' has same length and orientation as TA. And thus ZC' and TA have same length and orientation.
Successively translating the patch by vector TZ and -TZ = ZT we obtain a stripe bordered by two horizontal lines. Obviously the plane can be tiled by these stripes.

Appendix 1

Size of the nonagon

The hight h of the nonagon is defined as the vertical distance of the vertices Z and V.
h = 2w = 2cot(ε/2)
That means the height of the nonagon is a strictly monotonic decreasing function of ε.
The height can be very large for small ε.

Say u is the distance between U and TA and b is the distance between B and AC. Then t_a := min(u, b) and t_r := min(u, b)/(2w) are the absolute and relative thickness of the nonagon (neck).

Appendix 2

Perfect Nonagon

A Voderberg Nonagon is called perfect if the distances u and b (see appendix 1) are equal.
As the values of t_a and t_r depend on the angle ε, there exists a unique perfect nonagon for each suitable ε.
In the table x_A and y_A are the coordinates of the point A.

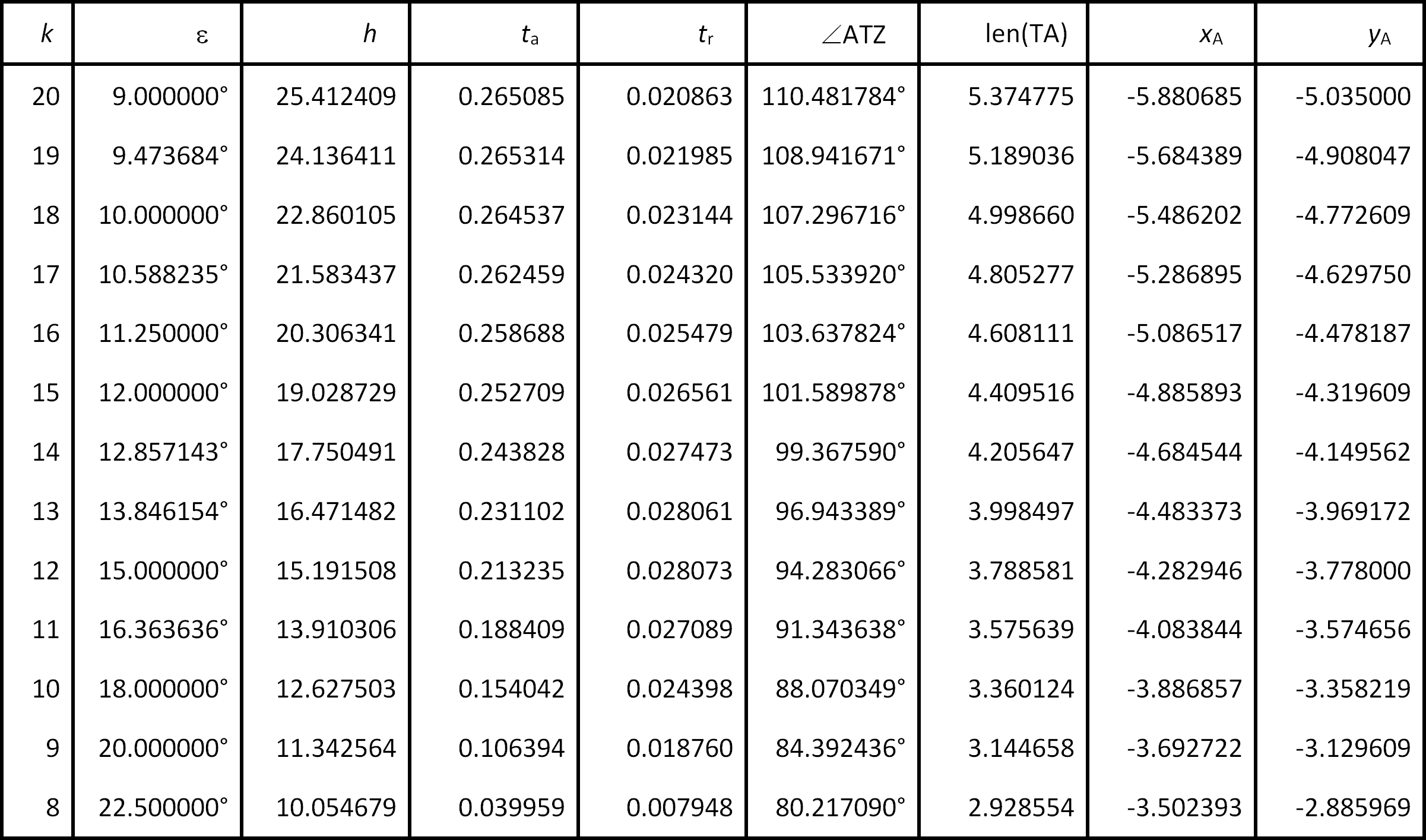
The relative thickness t_r of the nonagon neck is maximal for ε = 15°.

Appendix 3

Upper limit for angle ε

For ε = 23.90571178140393° the vertex U is an element of TA and the vertex B is an element of AR.