Can two rectilinear polygons surround two others?

Further Questions about Tetrads

20. Can two rectilinear polygons surround two others?

A rectilinear polygon is a polygon with sides parallel to the axes of Cartesian coordinates.
The question 20 was already considered by Alexander Thomas previous to 2011. [16]
It seems to be impossible to solve this problem without holes. Alexander Thomas used a rectilinear polygon with 24 edges to show that solutions with arbitrary small holes can be constructed. His tile was called Thomas-Trunk-Tile because it has a thin trunk.

Thomas-Trunk-Tetrad

Here another tile is shown with only 10 edges, although it does not lead to new mathematical insights.
We start with a polyomino of order 42, and define d as the thickness of the trunk, A as area of one tile, and H as area of one hole.

The thickness of the hole also is d. For the length of the hole we use 5d. With constant length s = 6 units for the left bottom horizontal edge of the yellow tile the construction is unique.
In the following sequence of tetrads the parameter d is decreased successively.
The area A of a tile is always greater than 36, whereas the area of the hole behaves like d².

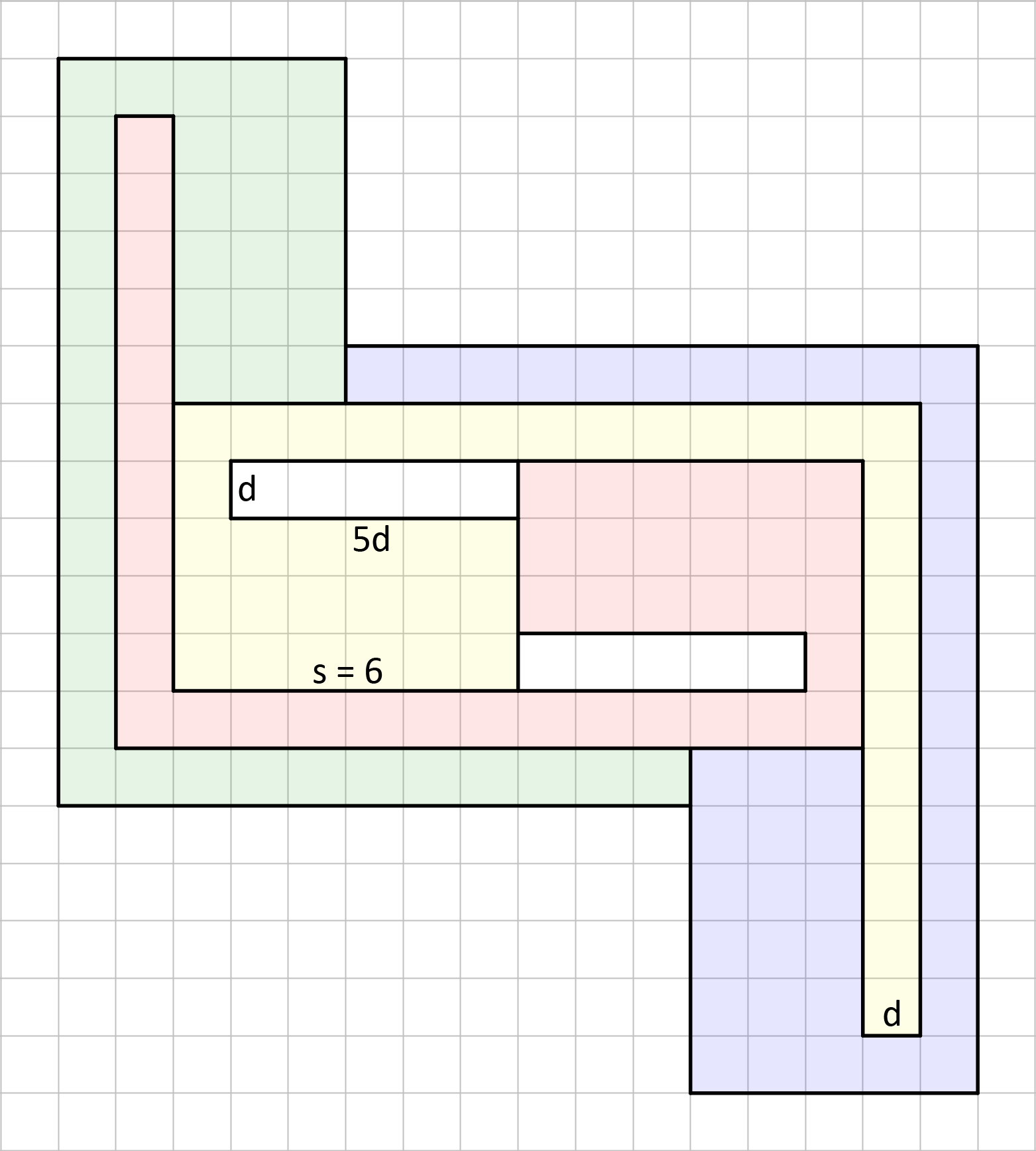
d = 1 H = 5 A = 42
d = 0.5 H = 1.25 A = 39
d = 0.25 H = 0.3125 A = 37.5
d = 0.1 H = 0.05 A = 36.6
d = 0.05 H = 0.0125 A = 36.3
d = 0.025 H = 0.003125 A = 36.15

                     Summary

 trunk thickness d   hole area H         tile area A      
 1                   5                   42               
 0.5                 1.25                39               
 0.25                0.3125              37.5             
 0.1                 0.05                36.6             
 0.05                0.0125              36.3             
 0.025               0.003125            36.15            
 0.01                0.0005              36.06            
 0.005               0.000125            36.03            
 0.0025              0.00003125          36.015           
 0.001               0.000005            36.006           
 0.0005              0.00000125          36.003           
 0.00025             0.0000003125        36.0015          
 0.0001              0.00000005          36.0006          
 0.00005             0.0000000125        36.0003          
 0.000025            0.000000003125      36.00015         
 0.00001             0.0000000005        36.00006         
 0.000005            0.000000000125      36.00003         
 0.0000025           0.00000000003125    36.000015        
 0.000001            0.000000000005      36.000006        
 0.0000005           0.00000000000125    36.000003        
 0.00000025          0.000000000000313   36.0000015       
 0.0000001           0.00000000000005    36.0000006       
 0.00000005          0.000000000000013   36.0000003       
 0.000000025         0.000000000000003   36.00000015      
 0.00000001          0.000000000000001   36.00000006

Obviouly it is possible to construct such a tetrad for arbitrary small holes.

Previous Question

Tetrads Contents

References