Tiling-Conjectures

Definition
In a tiling two different tiles A and B are adjacent if they share an edge.
In a tiling two different tiles A and B are neighbors if they share at least one point.

Conjecture 1

If a tile has only two adjacent tiles in a monohedral tiling of the plane, then the tile is a Voderberg tile of type 1 or 2.

Voderberg showed that all tiles with (2, 1)-enclosure property are of type 1 or 2 as described in his article from 1936.
Conjecture 1 is true, if Voderberg's conclusion is true. His spiral tiling of the plane contains infinitely many tiles with only two adjacent tiles (yelow tiles in Fig. 1). This is the main property of the Voderberg Spiral. Can you tell me any publication where this is mentioned?

Fig. 1. Yellow tiles have 2 adjacent tiles, light blue tiles have 3, and orange tiles have 4.

Conjecture 2

In a monohedral tiling of the plane, each tile has more than 2 neighbors.

Comments
Otherwise there has to exist a tile in the tiling that is completely surrounded by two other tiles.
A tile with two properties is necessary:
(1) The tile admits a tiling of the plane.
(2) There exists a patch with 3 copies of the tile, where one copy is completely surrounded by the others.

As far as we know, only the V-Dragons meet these conditions.
Definition
A dragon patch consists of three V-Dragon tiles with an inner tile A, a tile B that is a 180°-rotation of tile A, and tile C that is a rotation of A by an angle ε < 30°.

For a proof of the conjecture it would be sufficient to show:
(a) Each patch of 3 tiles where one tile is completely surrounded by the others is a dragon patch.
(b) There exists no monohedral V-Dragon tiling in which a dragon patch occurs.

Note: It is easy to find a tile that can be completely surrounded by two copies of itself as long as we allow holes in this composition.

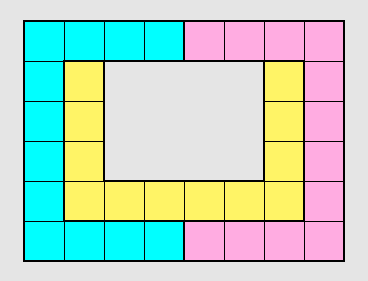
Are there tiles that admit a monohedral tiling of the plane, in which a tile with only 3 neighbors occurs?

A monohedral patch formed by 4 tiles, where one tile is completely surrounded by the other 3 tiles is also called Tetrad.
Tetrads are known since the 1970s.
Up to simple transformations we only know one tetrad that can tile the plane. This tetrad consists of 4 congruent tetrahexes.
But it is not necessary that the whole patch can tile the plane, it is sufficient that the tile can tile the plane and that in this tiling occurs at least one tetrad.

The yellow tiles have only 3 neighbors.
The other tiles have 7 or 8 neighbors. The average number of neighbors is (3+7+8)/3 = 6.

A possible transformation: Replace each hexagon with 7 hexagons.

There exists another tetrad formed by deciamonds. Amfirifma exhibits that this deciamond can tile the plane including tetrads. Two tiles are added to the tetrad and form a shape that tiles the plane. The tetrad itself cannot tile the plane.

The yellow tiles have only 3 neighbors.

Open problem: Does there exist a tetrad formed by polyomino tiles. Where the tiles admit a tiling of the plane that includes the tetrad?