Transformations and standard positions

(The following transformations work on magic and on bimagic 8x8-squares.)

8 basic transformations of squares

Due to rotations and reflections each square can be written in 8 different aspects.
Each of these 8 aspects is considered as the same unique square.

The standard position of unique magic squares

The standard position of unique SQ (or SM) is defined with the four corners:
Condition 1: A1 < A8, H1, H8 (A1 has to be the smallest corner number)
Condition 2: A8 < H1

Condition 1 can be fulfilled by rotations of the square.
Condition 2 can be fulfilled by reflecting the square at the left main diagonal.
(= swapping the coordinates x and y)

192 magic transformations for 8x8-squares

Some geometrical transformations always lead to another unique magic square when they are applyed to any simple magic square.
That means transformed magic squares are still magic. Therefore we speak of magic transformations.
Magic transformations do not change the set of numbers in any row, column or main diagonal.
They may only change the positions of the numbers within the row, column or main diagonal.

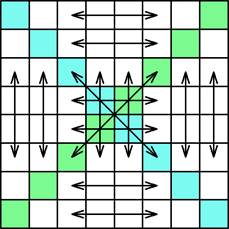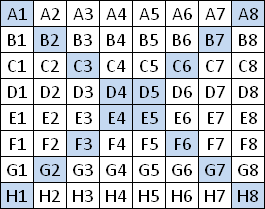
You can interchange any line x with the line (9-x).
The picture shows the permutation of line 3 with line 6.
In the notation of Benson and Jacoby: 1-2-6-4-5-3-7-8.
Of course you can use any combination of these 4 simple permutations.
There are 2⁴ = 16 transformations of this type A.

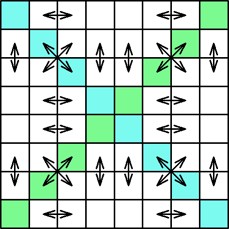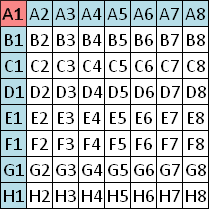
You can apply any permutation to the lines 1,2,3,4.
But you have to do the same with the lines 8,7,6,5.
The picture shows the permutation 1-3-2-4-5-7-6-8.
There are 4! = 24 transformations of this type B.

You may expect that from each magic 8x8-square you can get a set of 16 x 24 = 384 squares by magic transformations.
But for each square there is also the 180°-rotated aspect of the square in this set.
Therefore the number of magic transformations on 8x8-squares is 192.

The standard position of essentially different magic 8x8-squares

Two different unique magic 8x8-squares are called essentially different if it is not possible
to transform one square into the other square by magic transformations.

The standard position of ess. diff. SQ is defined with the entries of the two main diagonals:
Condition 1: A1 is the smallest of all integers in the two main diagonals.
Condition 2: B2 < G7, C3 < F6, D4 < E5
Condition 3: B2 < C3 < D4
Condition 4: A8 < H1

By magic transformations of type B you can move the smallest number into a corner. (4 possibilities)
By rotations you can move the smallest number in the upper left corner. (4 possibilities)
By magic transformations of type A you can fulfill condition 2. (2³ = 8 possibilities)
By magic transformations of type B you can fulfill condition 3. (3! = 6 possibilities)
By reflection you can fulfill condition 4. (2 possibilities)

Total possibilities: 4 x 4 x 8 x 6 x 2 = 1536 = 8 x 192 (8 basic and 192 magic transformations)

406 425 600 semi-magic transformations for 8x8-squares

In a semi-magic square only the rows and columns have to be magic.
Therefore semi-magic squares are invariant under any permutation of rows and independently of columns.
In a semi-magic 8x8-square you can do 8! permutations of rows and 8! permutations of columns.
As we have to exclude flippings of the whole square there are 8! x 8! / 4 = 406 425 600 semi-magic transformations.

The standard position of essentially different semi-magic 8x8-squares

Two different unique semi-magic 8x8-squares (SM) are called essentially different if it is not possible
to transform one square into the other square by semi-magic transformations.

Our standard position of ess. diff. SM is not compatible
with the standard position of unique magic squares:

Condition 1: A1 = 64 (A1 is greater than any other integer in the square)
Condition 2: A1 > A2 > A3 > A4 > A5 > A6 > A7 > A8
Condition 3: A1 > B1 > C1 > D1 > E1 > F1 > G1 > H1
Condition 4: A8 < H1

Possibilities: 64 x 7! x 7! x 2 = 8 x 406 425 600

The complement transformation

This transformation is not a geometrical transformation, it works on the integers j.
The transformation works on semi-magic, magic and bimagic squares.
In an order-8 square each entry j is replaced by (65-j).

Symmetrical magic squares are invariant under the complement transformation.
That means the transformation leads just to another aspect of the same unique magic square.

Moreover the complement transformation can lead to a transformed square which is not essentially different from the original square.
We call these squares complementary invariant.

Back to Bimagic 8x8-Squares