|
How to count magic series
|
Very small orders (m ≤ 7)
Did you manage to find all 86 magic series of order 4? If yes: congratulations. If no: here is the complete list.
Probably you don't want to search the 1394 magic series of order 5, do you?
Already in 1942 Maurice Kraitchik determined the number of magic series up to order 7.
A great achievement - imagine that there are nearly one Million magic series of order 7. (To be precise: N(7) = 957332)
(Maurice Kraitchik, "Magic Series." §7.13.3 in Mathematical Recreations. New York: W. W. Norton, pp. 143 and 183-186, 1942.)
Small orders (m ≤ 12)
When I showed my paper 'theory of magic series' to a (magic squares) friend, he said
'I wonder why you need all this theory.' and sent me an old Basic program:
10 for a=1 to 13
20 for b=a+1 to 14
30 for c=b+1 to 15
40 for d=c+1 to 16
50 if a+b+c+d=34 then n=n+1
60 next d
70 next c
80 next b
90 next a
100 print n
My friend added the line: 'And this type of program can be easily used for any order.'
He is right, in principle the problem can be solved by his algorithm.
But he did not consider how much time it takes for a computer to complete that task for orders greater 12.
Say the inner for-next-loop can be done 1,000,000,000 times in one second (an incredible fast computer).
Then we would be able to count about 3 · 1016 magic series within one year.
Enough to determine the number 2.1 · 1016 of magic order-13 series.
But the time increases fast:
order 14: 57 years
order 15: 4900 years
order 16: 460,000 years
order 17: 47,000,000 years
Of course, the shown program can be improved. And it has the advantage that the series were determined explicetely,
they can be saved and used for constructing magic squares.
But orders greater 13 can't be achieved with such types of algorithms.
Order m ≤ 100
As far as I know Henry Bottomley was the first who found an iterative algorithm that determines the number of magic series.
His algorithm calculates generally the number of partions of large numbers.
Look at his excellent and well commented JAVA program that is called
partition calculator (external link).
Independent from Bottomley but certainly some months later in September 2002 I found a similar approach that
consideres magic series only. Both algorithms use a two-dimensional array which gets very large for higher orders.
I did all calculations in gb32 an exotic German programming language.
The following small C++ program was just written to demonstrate the iteration method:
Download the source code or the executable magic-series.exe
You can't understand the code without reading the pdf file 'Theory of Magic Series'.
The results have only an accuracy of 15 digits. To get exact numbers you have to implement big integer procedures.
Don't use the program for orders above 50 if you haven't got more than 1 GByte RAM.
You first have to program the continuousely saving and reading of array portions on a hard disk.
Such a task really punishes your hard disk - save important data before you do such things.
And note: It is not a good idea to leave this task up to the virtual memory of your OS.
Order m > 100
In an email (2005-02-02) Henry Bottomley sent me an experimental approximation of the number of magic series.
In another email (2005-02-09) he gave me the permission to publish his formula:
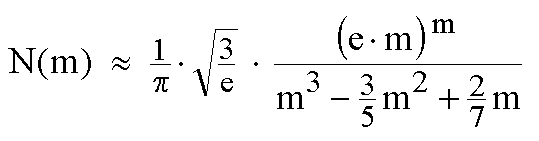
This experimental formula is really excellent. The relative error decreases continuously with higher orders.
For m = 100 this relative error is nearly as low as 10-7.
Walter Trump, Nürnberg, Germany, (c) 2005-02-08 (last modified: 2005-02-11)