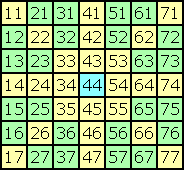
The blue centre-cell has the adress (4,4) or 44. I call the 24 yellow cells axis-cells and the 24 green cells filling-cells. It is of great importance to divide the square without centre-cell in these two segments.
| Ultramagic Squares of Order 7 |
| Cells |
 |
The 49 cells of an order-7 magic square are adressed by two coordinates x and y.
Cell (x,y) or shortly xy is situated in row x and column y.
The rows and columns were counted from 1 to 7.
The upper lefthand cell has the adress (1,1).
(Only for special purposes like transposition-formula we also use coordinates x, y from 0 to 6.)
The square on the left shows the adress of each cell. The blue centre-cell has the adress (4,4) or 44. I call the 24 yellow cells axis-cells and the 24 green cells filling-cells. It is of great importance to divide the square without centre-cell in these two segments. |
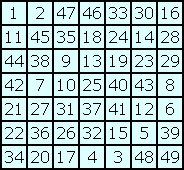
| It is usual to fill the cells of a 7x7-squares with consecutive natural numbers from 1 to 49. I use this way for printing squares but not for calculating squares. The square on the left is self-complementary and pan-magic. n(x,y) is the number in cell (x,y). For example n(6,5) = 12 in this square. n(4,4) = 25 in each self-complementary 7x7-square. Two numbers located symmetrically about the centre-cell sum up to 50. This could be expressed by the equation n(x,y) + n(8-x,8-y) = 50. |
|
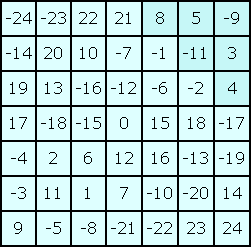
The cells of the square on the left are filled with whole consecutive numbers from i(x,y) = n(x,y) - 25 is the integer in cell (x,y). This numeration has many benefits for the calculation of odd-order magic squares. i(4,4) = 0 in each self-complementary 7x7-square. Integers with the same absolute value a(x,y) = |i(x,y)| are located symmetrically about the centre-cell: i(x,y) = -i(8-x,8-y) or a(x,y) = a(8-x,8-y). The integers in each column, row or diagonal add up to zero. You get a homogeneous system of equations. There are derived equations that contain only 6 variables. The sums of several 6-cell-triangles are zero in each self-complementary pan-magic order-7 square. See for instance the upper righthand triangle of the square on the left: 8 + 5 - 9 - 11 + 3 + 4 = 0 |
| summary | cells | equations | transpositions | improvements |
| results | programs | files | conclusions | samples |