ultramagic squares of order 7

Ultramagic Squares of Order 7

Transpositions

Introduction

Let M₇ be the set of all 7x7 matrices containing the first 7² natural numbers, respectively the whole numbers from -24 to 24.
A (matrix-) transformation T is an injective (one-to-one) function T: M₇ --> M₇.
A transposition P is a transformation that is given by a definite permutation of the matrix elements.
For instance P(x,y)-->(8-x,y) describes the reflection of the squares (matrices) with respect to their middle column. Let s be a magic square (matrix) then P(s) is the reflected square.
Two transpositions U and V build a new transposition U·V by first applying V and then U to the squares. The set of all transpositions is a non-commutative group with respect to the described connection. The neutral element is the idendity I. As transpositions are injective functions, for each T exists a T^-1 with T^-1·T = I.

General Square-Transpositions

The 3 rotations and the 4 reflections of the squares build together with the idendity I a sub-group RS with 8 elements.
The 90° clockwise rotation shall be called R. The reflection at the middle row shall be called S. R and S generate the sub-group RS.
Two squares that could be transformed to each other by a transposition from RS are meant to be equivalent. A set of squares is called unique, if its elements are pairwise non-equivalent.

Special Transpositions

There is another sub-group containing 6 transpositions. This sub-group could be generated by a single transpostion, that I simply call K.
K does not desturb the pan-magic and the self-complementary property of a 7x7-square. K interchanges the rows with the upwards diagonals and the columns with the downwards diagonals. Therefore the transposed square is still pan-magic.

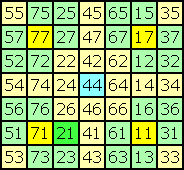
Examine square 0 below. The rows and columms are numbered from 1 to 7. The cell with the adress xy is in column x and row y. Each cell is filled with the number that equals the adress of the cell. Of course these numbers do not produce a magic square.

By the transposition K the numbers are placed in other cells. The new arrangement could be find in square 1. The numbers in two cells that are positioned symmetrically to the centre-cell always sum up to 88, just as in square 0. Thus the square is still self-complementary.

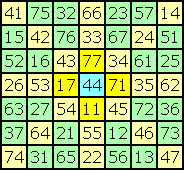
Another apply of K leads to square 2. It shows that K² is a non-cyclic permutation of rows and columns in the order 5-7-2-4-6-1-3.
Examinations of square 3 show that K³ is an involutoric transposition, i.e. K³·K³ = I. The values of the original square stay in their cell or are pairwise interchanged.
As you can see in square 4, K⁴ is another non-cyclic permutation of rows and columns in the order 6-3-7-4-1-5-2.
K⁵ is equal to K^-1, the invers transposition of K.

	---> K		---> K		---> K
Square 0		Square 1		Square 2

	---> K		---> K
Square 3		Square 4		Square 5

Transposition-Group

The transpositions R, S and K generate a group of 48 different transpositions. One known order-7 square could be transposed into 47 other squares. If e is the total number of self-complementary pan-magic 7x7-squares then d = e / 8 is the number of unique squares (i.e. without rotated and reflected squares). But it is enough to count all essentially different squares c = e / 48. All other squares could be derived by applying a suitable transposition.

Axis-Cells

K transposes each of the 24 yellow axis-cells to another axis-cell. Now look at the four numbers (11, 71, 17, 77) in the corner-cells of square 0. Notice that these numbers move through all yellow axis-cells by continued applying of K.
Assume the number 1 is placed in any axis-cell. Then you always are able to move the number 1 to one of the corner-cells. If necessary an additional rotation brings the number 1 into cell (1,1).
You need no reflection for this process. The square could be reflected at the downwards main diagonal to interchange n(2,1) and n(1,2) without changing n(1,1). Thus counting all squares with n(1,1) = 1 and n(2,1) < n(1,2) is enough to get the total number of all squares with 1 in any axis-cell.

Filling-Cells

K transposes each of the 24 green filling-cells to another filling-cell. Look at the number 21 in the squares 0, 2 and 4 that were produced by applying K² once, twice or not at all. With rotations and reflections number 21 could be moved from these positions to all other filling-cells.
Thus n(2,1) could be moved to any filling-cell by applying one of the 24 transpositions of the sub-group that is generated by R, S and K².
As you see in square 3, K³ interchanges n(1,1) and n(4,6), without changing n(2,1). Thus counting all squares with n(2,1) = 1 and n(1,1) < n(4,6) is enough to get the total number of all squares with 1 in any filling-cell.

Formula of the transposition K

K(x,y)=(v,w) means that the transposition K moves the number from cell (v,w) to cell (x,y).
In the first formula x,y ranges from 1 to 7.

K(x,y) = ( (y - x + 10) Mod 7 + 1 , (y + x + 2) Mod 7 + 1 )

The formula could be shortened by using coordinates x, y from 0 to 6:

K(x,y) = ( (y - x + 10) Mod 7 , (y + x + 4) Mod 7 )

Reducing all calculations to the cyclic group (0, 1, ... 6), i.e. modulo 7, you get:

K(x,y) = ( y - x + 3 , y + x - 3 )

This formula could be easily extended to other squares with odd order N = 2m + 1 and x, y from 0 to N-1, calculating modulo N:

K(x,y) = ( y - x + m , y + x - m )

More transpositions

In June, 2004 the French engineer Francis Gaspalou reported another transposition for ultramagic squares of order 7. See improvements.

Reference

Transposition for pan-magic squares that are similar to K², K³ and K⁴ are mentioned in the following very interesting book:
'New Recreations with Magic Squares', William H. Benson and Oswald Jacoby, Dover Publications, Inc., New York 1976

Index

summary	cells	equations	transpositions	improvements
results	programs	files	conclusions	samples