Can the outline of a Tetrad form a regular polygon?

Further Questions about Tetrads

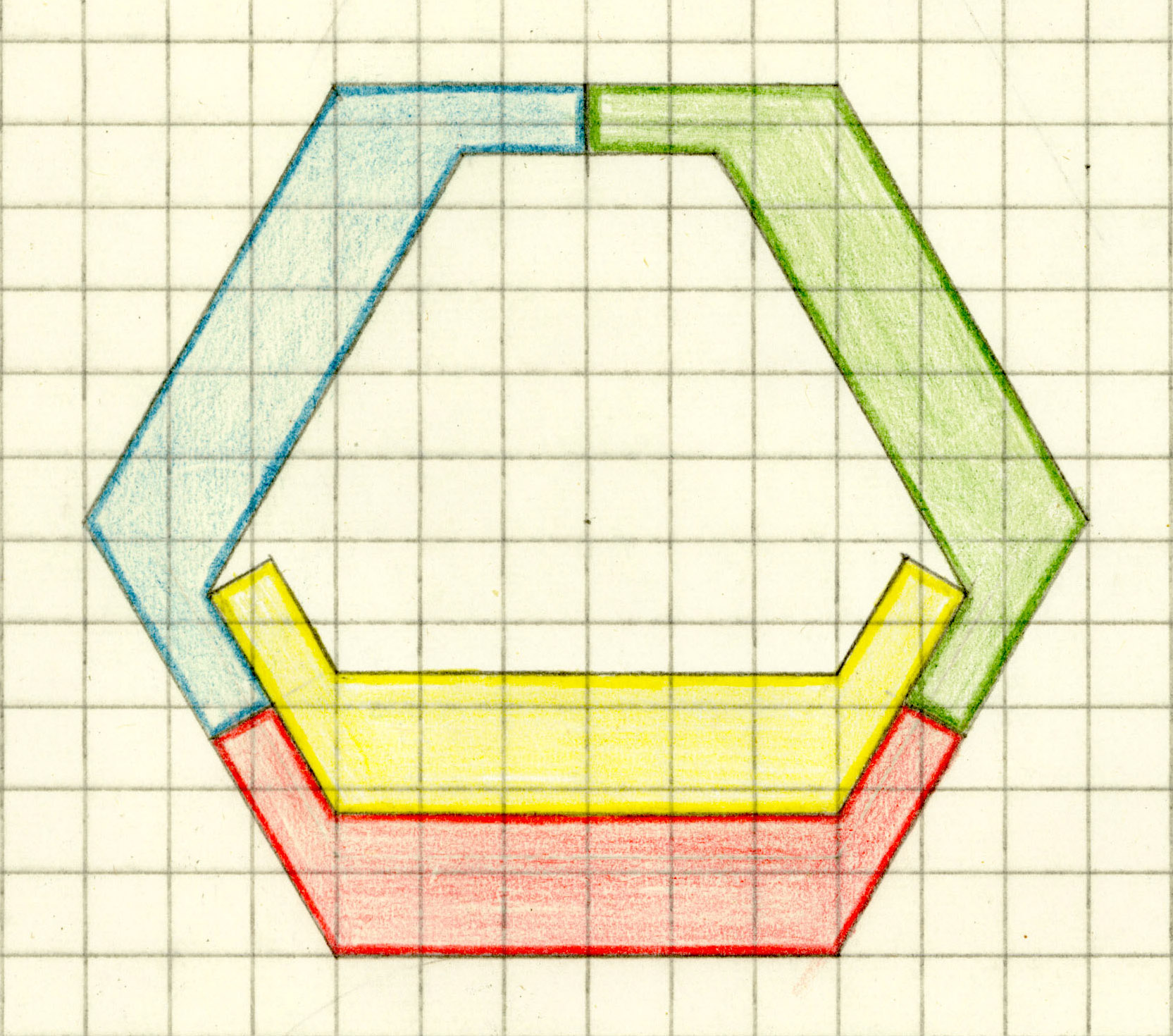
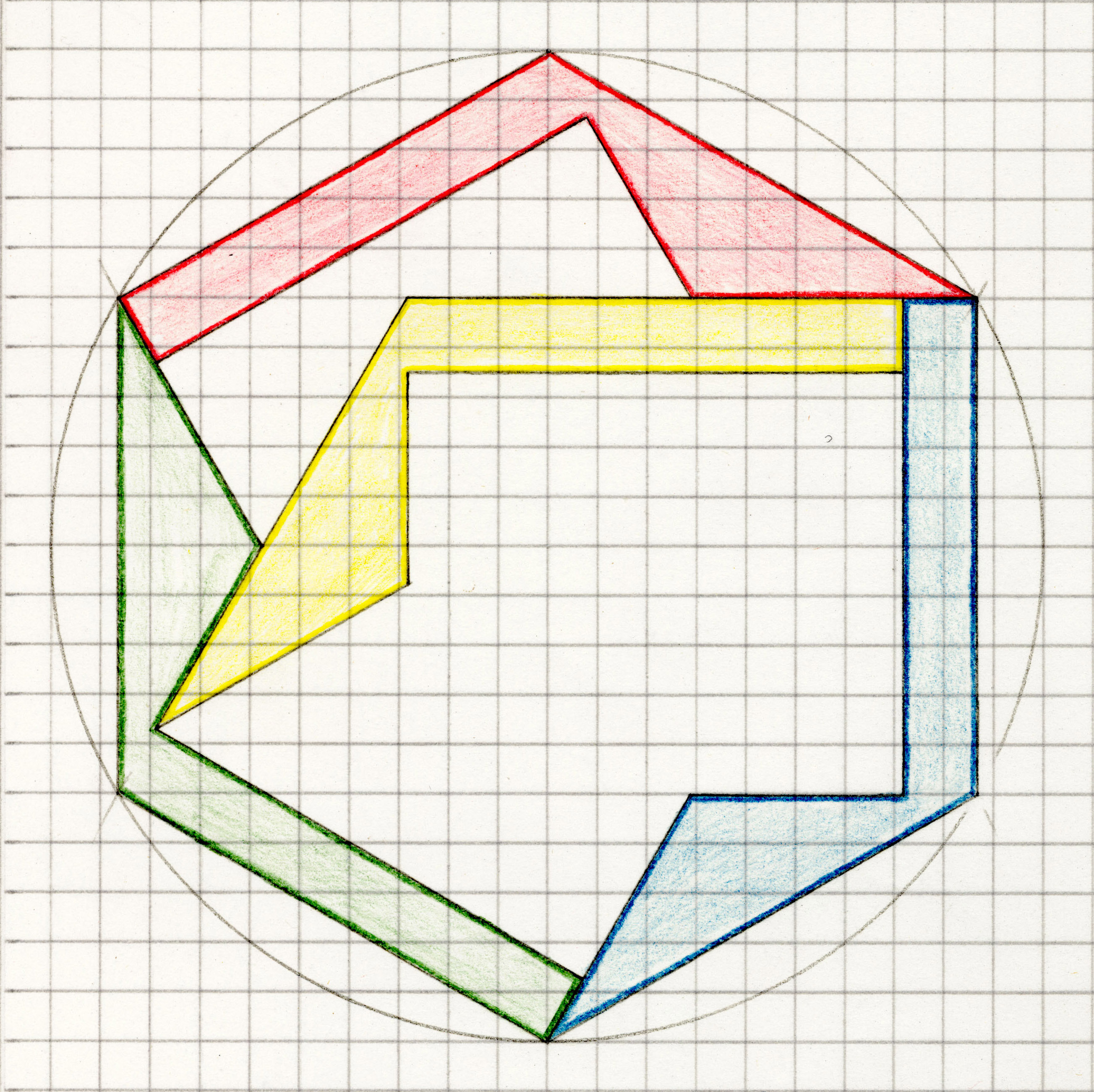
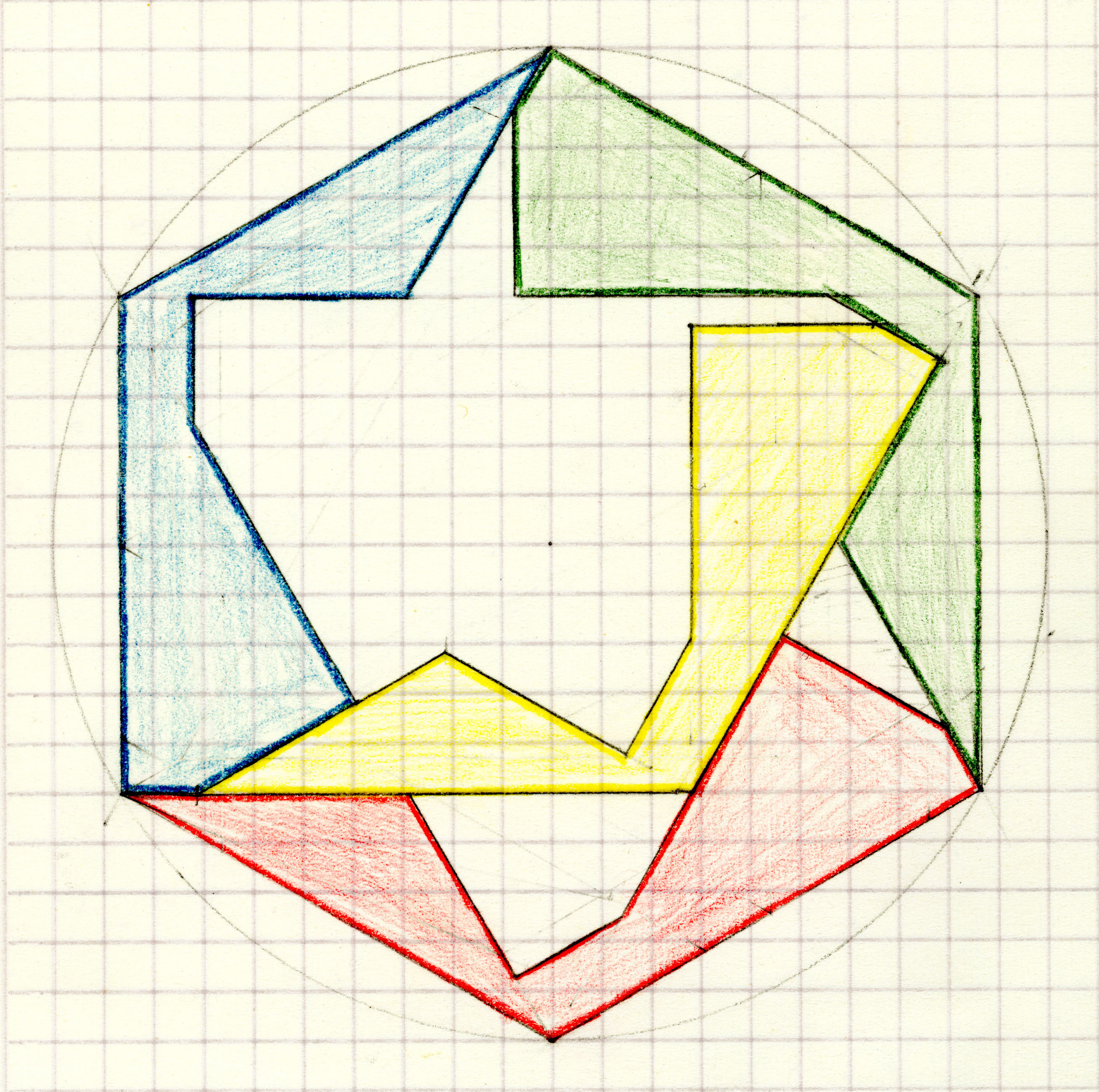
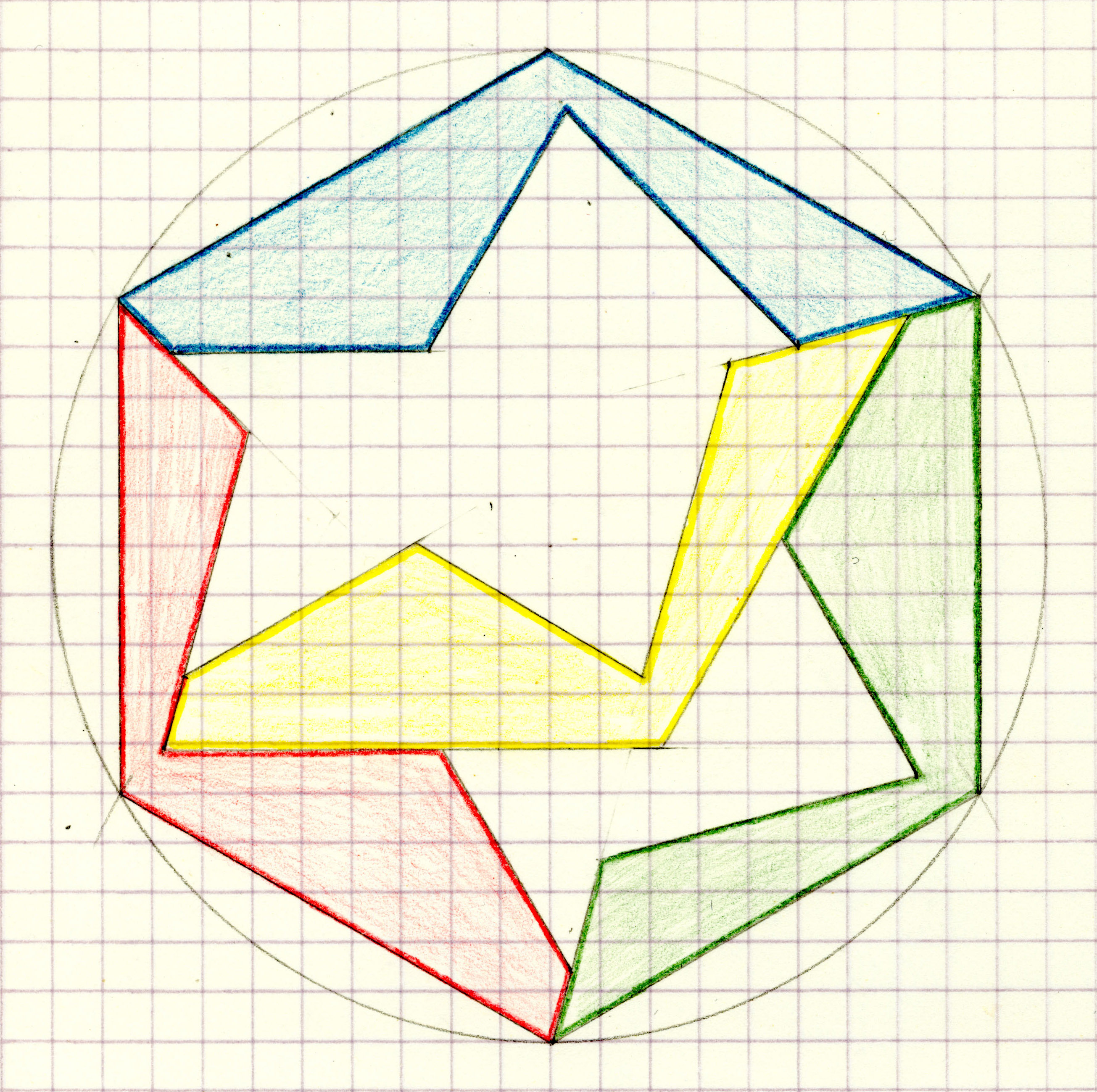
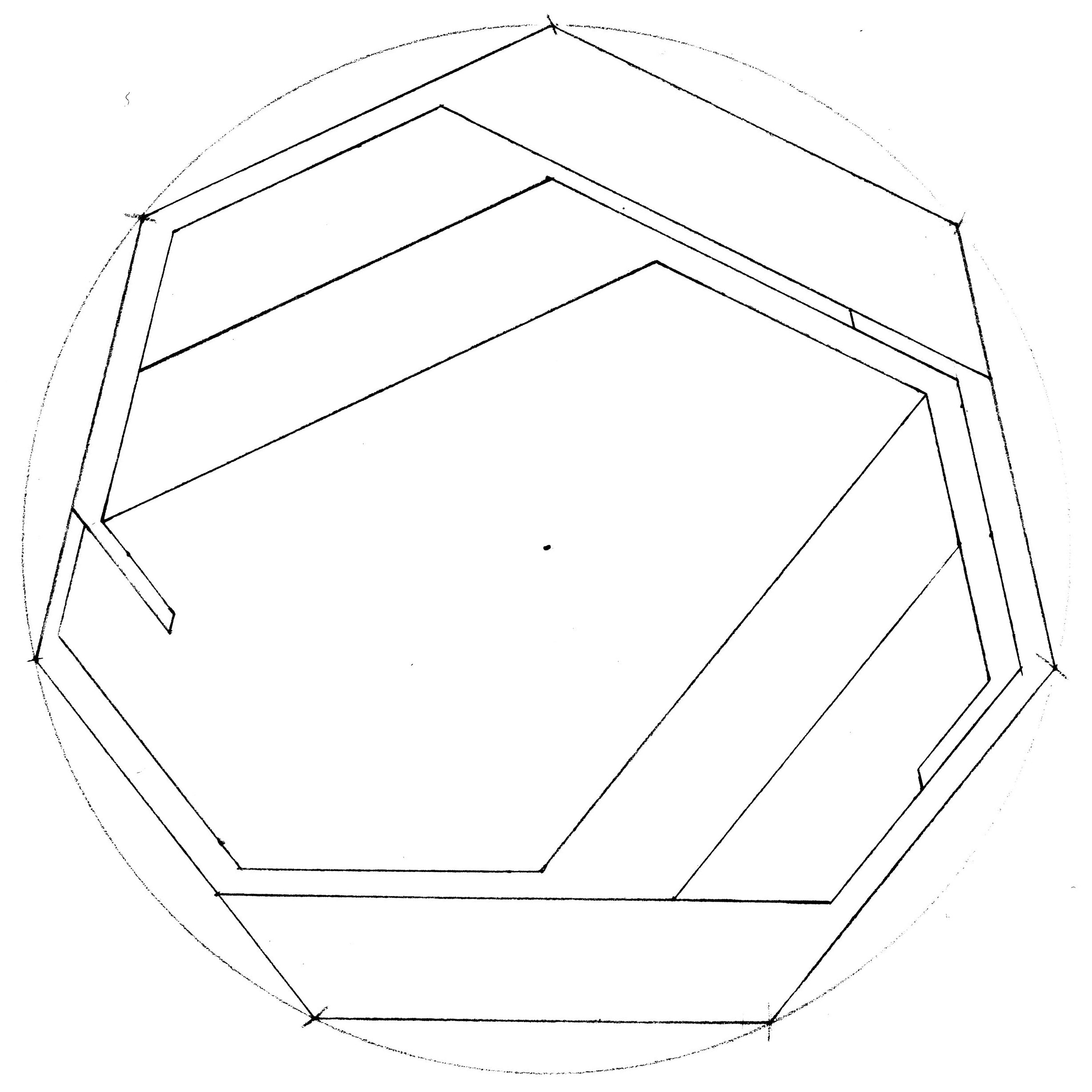
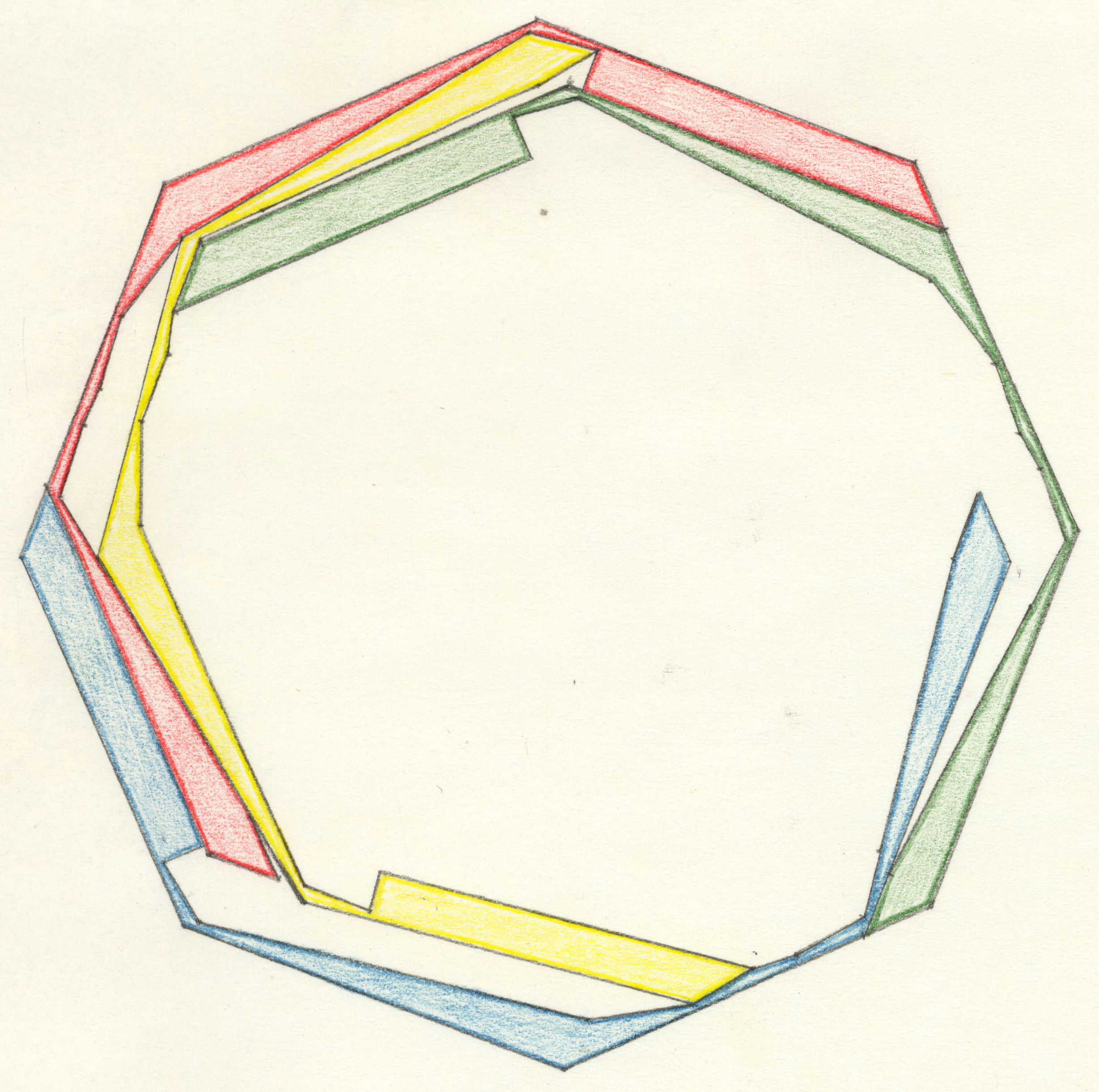
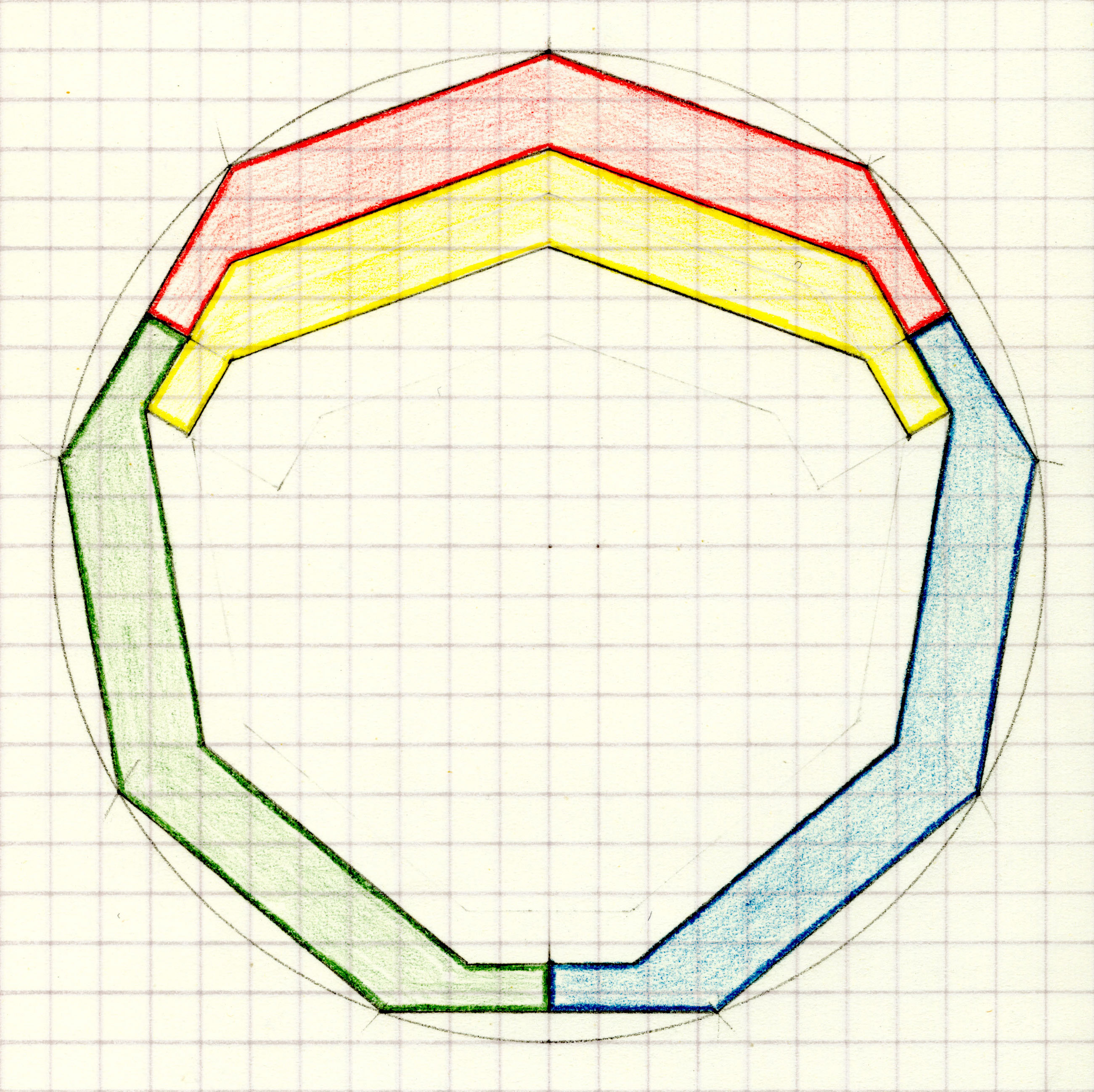
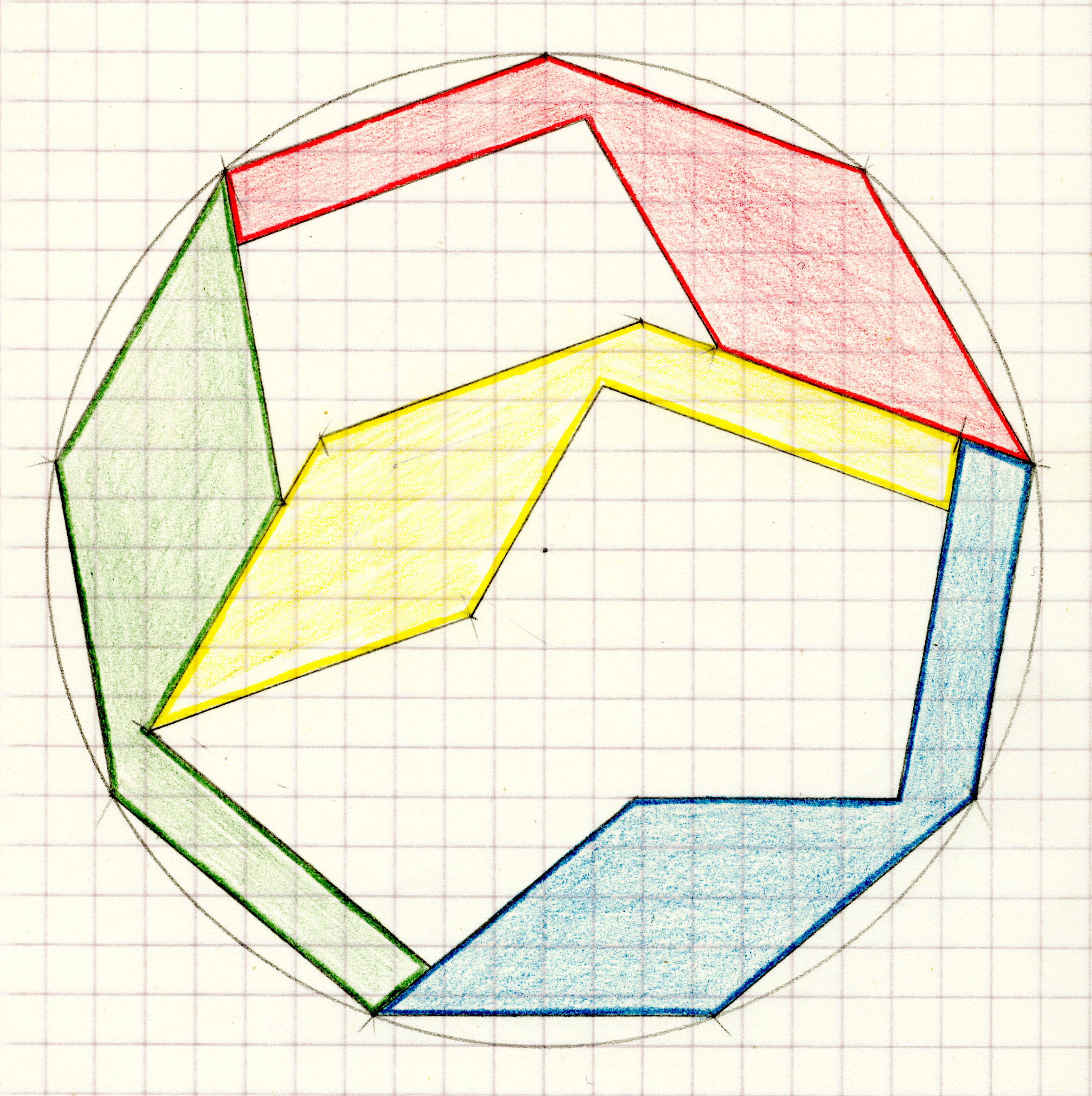
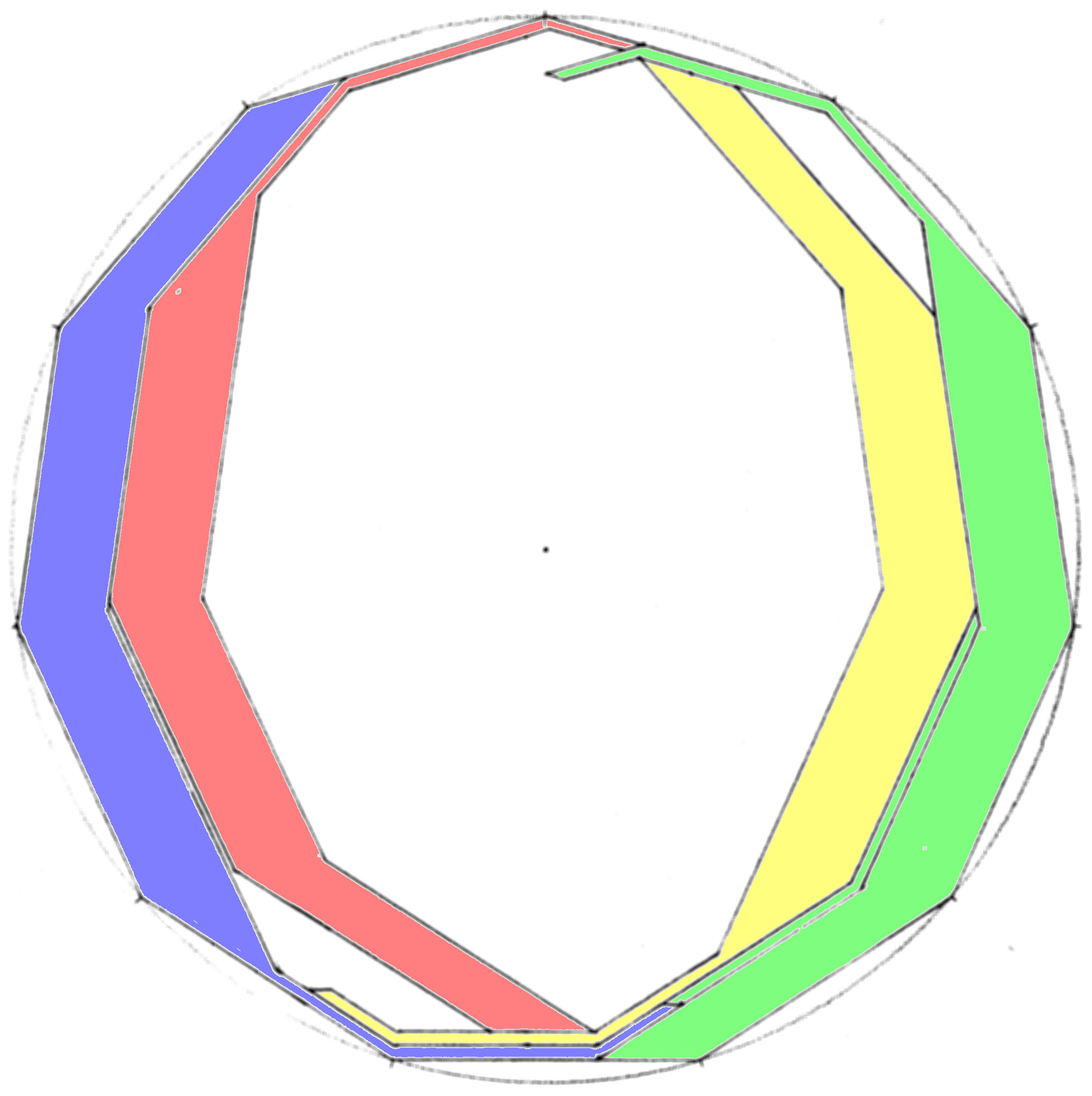
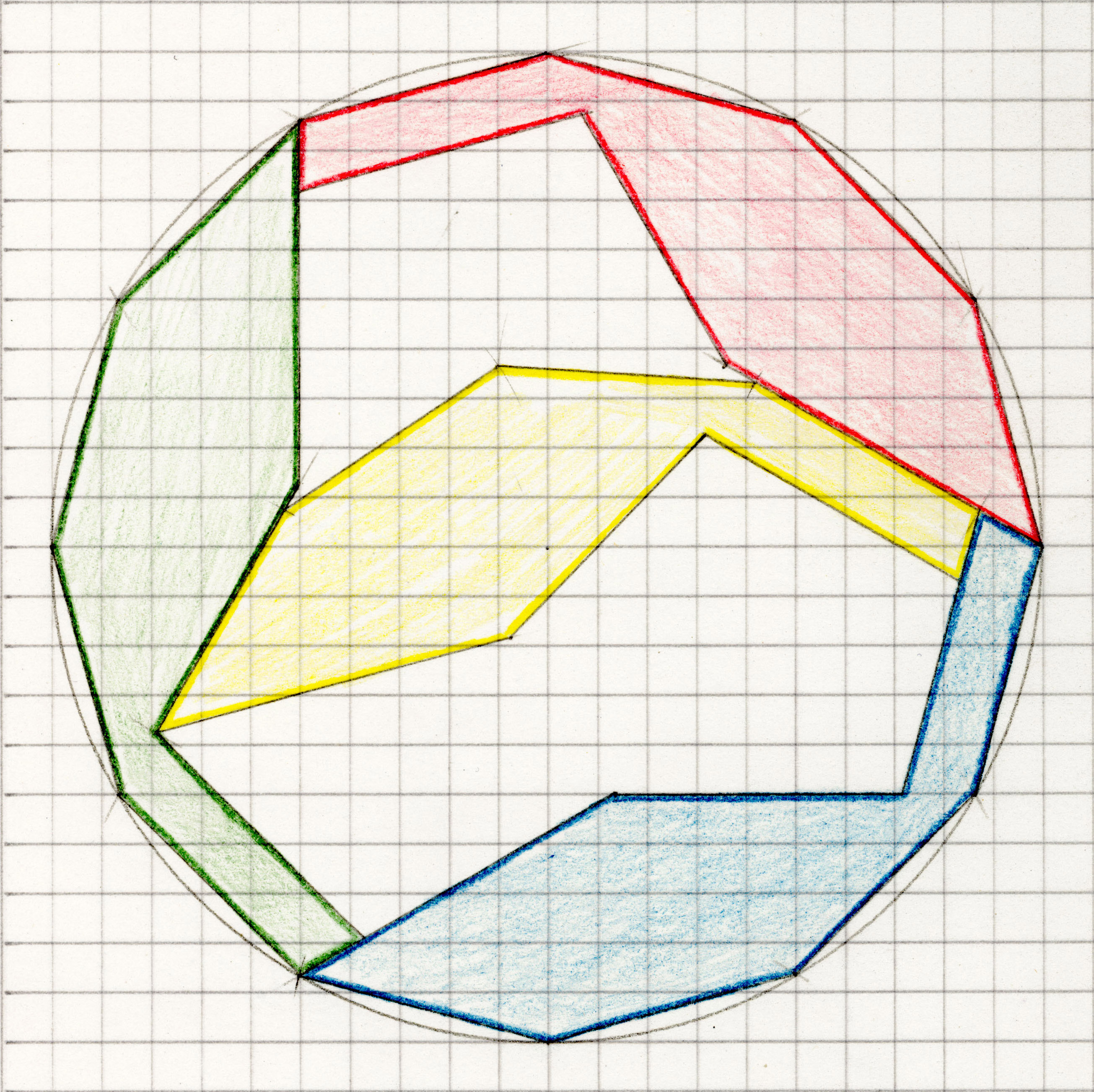
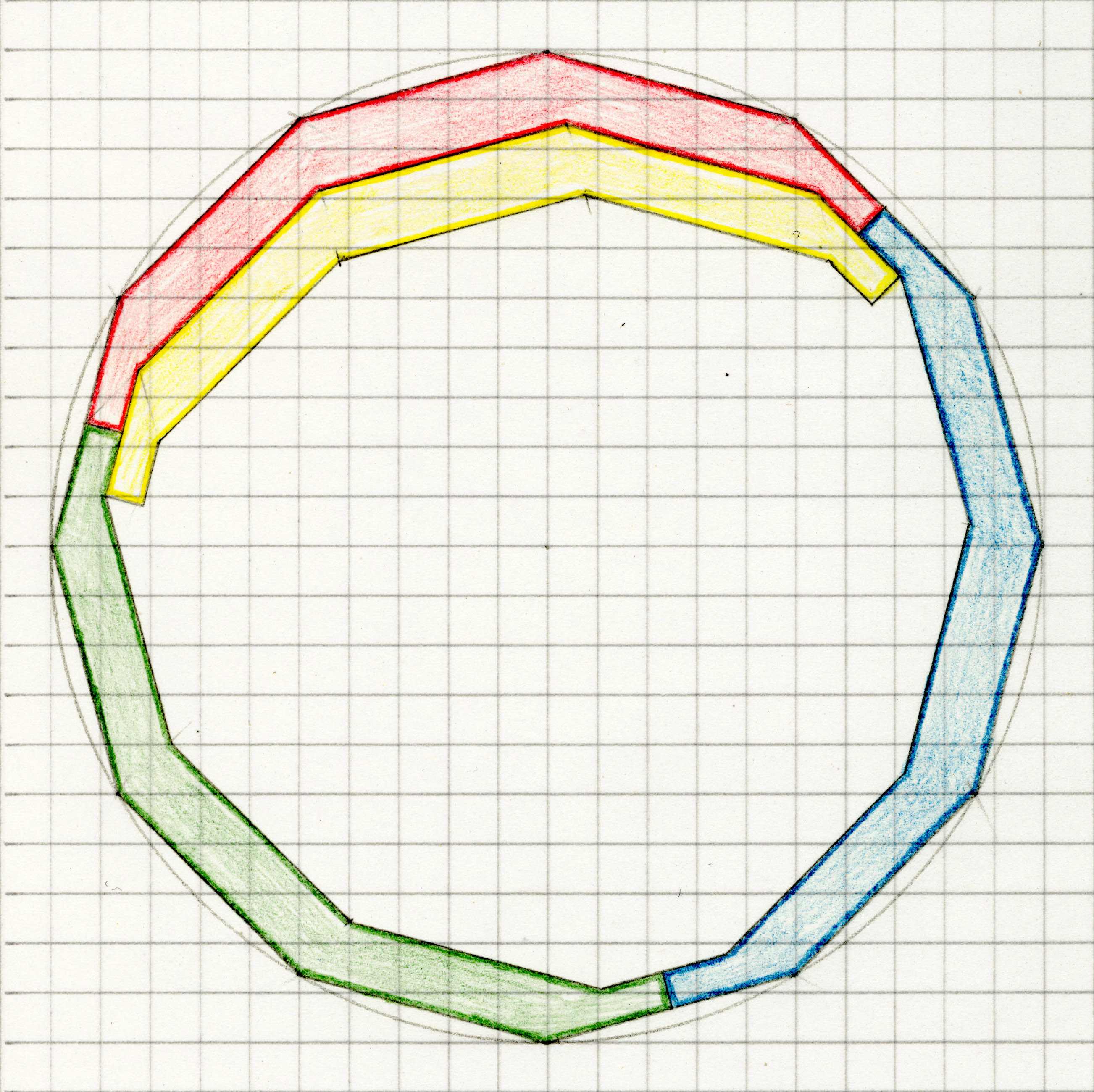
10. Can the outline of a Tetrad form a regular polygon?

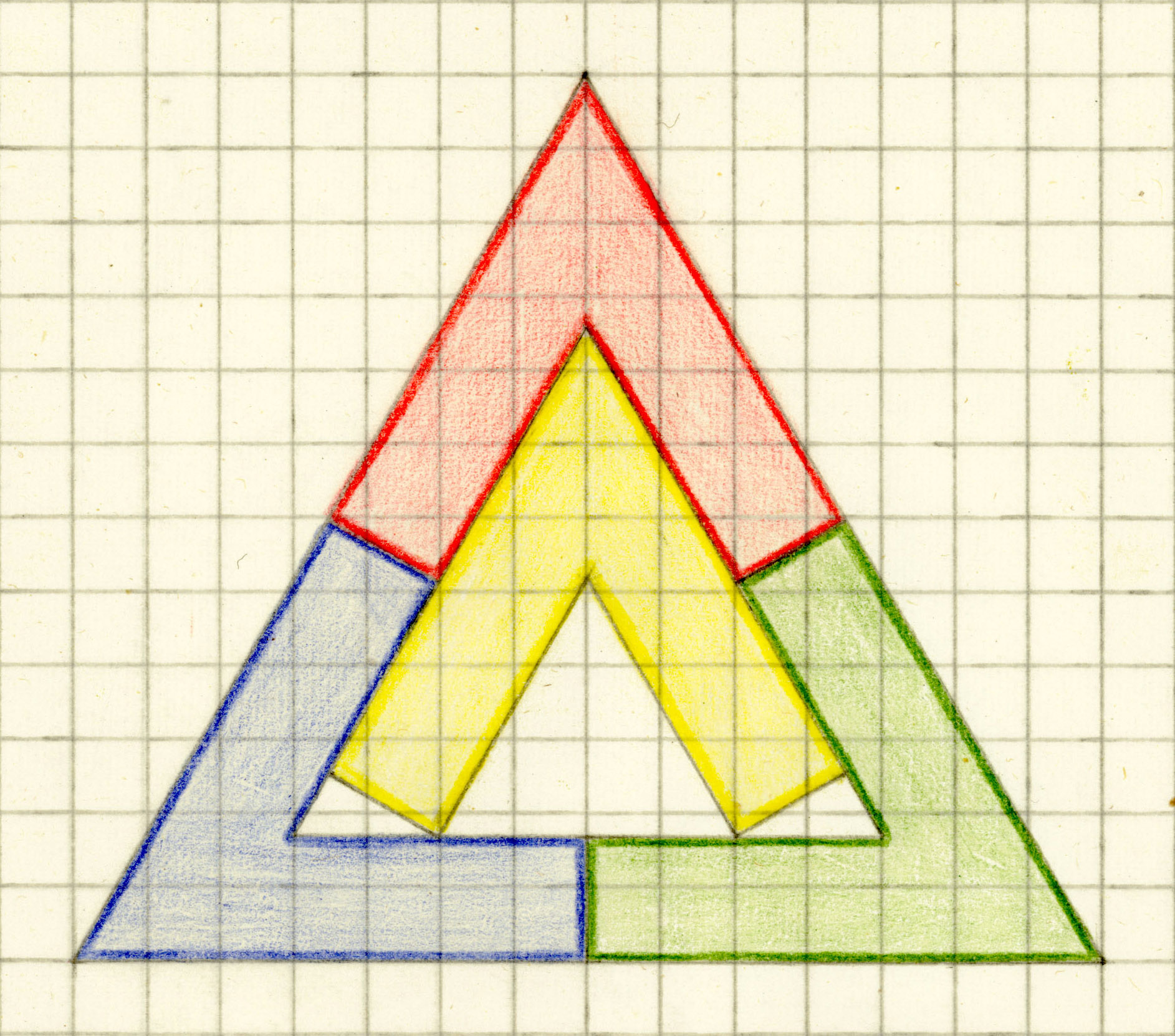
Yes: This seems to be possible for all polygons of order n, except when n = 4.

n = 3 Triangle

Open problem (until 2025-01-17): Can triangles which are not equilateral be the outer boundary of a tetrad?

Henry Zhang could answer this question in January 2025 by creating a tetrad where the outer boundary is an isosceles right triangle.
His solution consists of four congruent octagons and he also provided a drawing with details of his construction.

Zhang's tetrad can be transformed into a tetrad with mirror symmetric tiles. But this increases the empty area inside the tetrad.

n = 4 Square

The picture just shows that it is impossible to create a square tetrad where the outline is formed by only two tiles. The sum of the two short lines is smaller than 1. A complete proof is not given here.

The problem is easy to solve for rectangles with width < length < 2 · width and for parallelograms.

Open problem: Which trapezoids or kites can be the outer boundary of a tetrad?

n = 5 Pentagon

The next figure shows a possible construction principle and an incomplete solution, where the inner tile and the blue tile have only one point in common.

The problem can be solved. In the second solution the inner tile (yellow) has left its original position.

Another challenge is to minimize the area of the holes.

n = 6 Hexagon
This can be done with hexagon tiles. The first tetrad and its tiles are mirror symmetric.

You also can use heptagon tiles.

n = 7 Heptagon

GeoGebra vector graphic and old drawing

First construct the circle and the heptagon. Then the cyan (light blue) points with distance x from certain corners.
Then the magenta (dark red) points on the green and blue dotted lines.
It also is possible to use smaller values for x, then the yellow tile does not perfectly fit in the green tile.

n = 8 Octagon Should be proved

n = 9 Nonagon

n = 10 Decagon Should be proved

n = 11 undecagon Should be proved

n = 12 Dodecagon

Previous Question

Tetrads Contents

Next Question