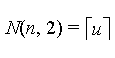
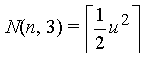
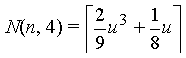
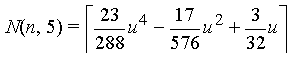
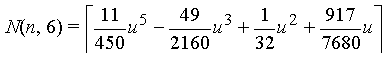
magic series - Magic series formulae

Magic Series

Formulae

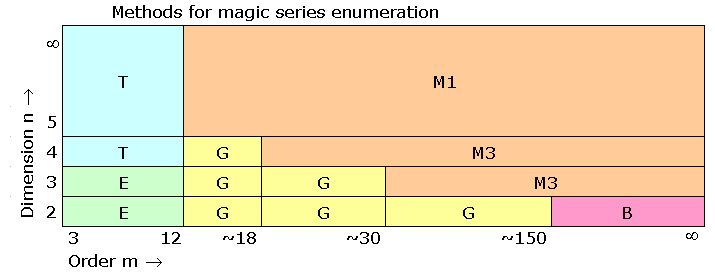
Number N(n, m) of magic series for hypercubes of dimension n and order m

Afraid of high dimensions n ? Or high orders m ?
Read that there are no longer any limits for the calculation of N(n,m).
Even if you don't like formulae go on reading. The story is rather exciting.

By examining all available data I found the following formulae in June 2006.
Until 2013 these were just experimental results, I could not prove the formulae for m > 3.
But Dirk Kinnaes found a proof in March 2013. Read about his surprising proof.

We need some easy definitions first:

The formulae for small orders m and random dimensions n

Order m = 2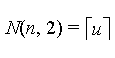
Order m = 3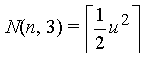
Order m = 4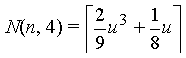
Order m = 5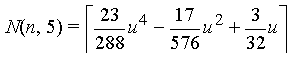
Order m = 6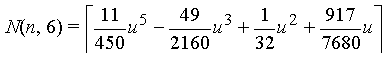

Orders 7 to 11

Read how the formulae were found: History of the magic series formulae

The first coefficients of the formulae

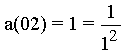
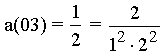
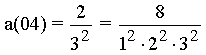
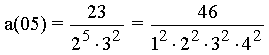
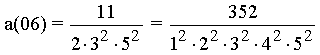
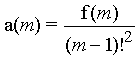The denominators of these coefficients can be written in a certain way:

a(07) to a(11)

Generally we can write for order m: with the numerator f(m).

The sequence of the numerators

We know the first terms of the numerator sequence f(m). Starting with f(2):

1; 2; 8; 46; 352; 3364; 38656; 519446; 7996928; 138826588; ?

But what are the next terms of this sequence?
On July 13^th, 2006 I asked that question to my French friend Christian Boyer and to my great surprise he could immediately continue the sequence:

...; 2683604992; 57176039628; 1331300646912; 33636118326984; 916559498182656; ...

His secret: He found the sequence at Sloane's encyclopedia of integer sequences A099765 and meant:

"All this is the proof that your coefficients are 100% correct and that they have a strong mathematical basis.
But... it will be perhaps difficult to explain WHY this sequence and formula is used for hypercubes."

The sequence was submitted in a completely different context by Benoît Cloître in November 2004.
(I speak about Cloître's sequence - not knowing who really invented this sequence.)

Cloître's sequence:

On January 3^rd, 2007 I found the formula for order m=12. The first coefficient has exactly the predicted value.
See formula N(n,12) and coefficient a(12)

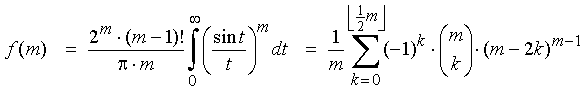The surprising proof

In 2006 I asked: Does anybody understand why the numerators are given by Cloître's formula?
I never thought that anybody will ever be able to answer with yes.
But on March 29^th, 2013 I received an email from Dirk Kinnaes, Belgium. He wrote:

"I think I have now actually found a proof, for the case that m is even, that N(x,m) is indeed a quasi-polynomial of degree m-1 in x, and that its coefficient of degree m-1 is indeed equal to f(m)/(2^(m-1) (m-1)!^2 ), where f(m) is the m-th term in the sequence defined in OEIS A099765.
My proof is based on geometric concepts, and in my mind it gives a clear geometric interpretation of all the terms and factors appearing in the expanded formula (with f(m) = the summation formula given in OEIS A099765).
I also prove that, for the case that m is even and m≥4, the period L(m) of the quasi-polynomial N(x,m) in x is a divisor of l(m-1), where l(n) is the least common multiple of the first n natural numbers (1,2,…,n).
All this seems to be true if m is odd as well, but adaptations of the current proof would certainly be necessary, if at all possible."

Please read Kinnaes' proof written in a very clear mathematical style. And read his geometrical interpretations too.

Dirk Kinnaes is a computer scientist, he lives in Genk, in the North-East of Belgium and works at the University of Leuven.

What about the other coefficients?

The results of Cloître's formula become zero, when the exponent is changed from (m-1) to (m-2).
The coefficients of u^m-2 in the magic series formulae are also zero.

With the exponent (m-3) the results of Cloître's formula are negative, just as the coefficients of u^m-3 for m ≥ 5.
Unfortunately I can't find any further relations.

Is anybody able to continue the sequence of the third coefficients (of u^m-3)?
When we use m!² as denominators the sequence of the numerators for m ≥ 4 is given by:
72, -425, -11760, -298900, -7590912, -200375910, -5562585600, -163144400430, -5059767398400, ...
See text-file third-coefficients-numerators.txt for more details and estimates.

Approximation of N(n,m) for high orders m and dimensions n

Some statements (experimental results):
- The terms of the sequence f(m) can be calculated easily.
- The second coefficients are zero.
- The absolute values of the third coefficients are strictly decreasing.
- The third coefficients are negative for m ≥ 5.

Thus we get good approximations of N(n, m) by just calculating the first summand of the affiliated formula.

Let's speak about 'm1-approximation' (First Member Approximation).

Example: N(100,100):
We get u ≈ 0.5·10²⁰⁰. That means u⁹⁹ is greater than u⁹⁷ by the factor 0.25·10⁴⁰⁰
Thus the third member of the formula is very much smaller than the first one. And our approximation will be rather accurate (about 395 digits). The 50 digits that were shown here should be absolutely correct.
    f(100) = 8.16246782510785755663036180811761134836314098272794... · 10¹⁸²
    (99!)² = 8.70978248908948007941659016194448586556972064394084... · 10³¹¹
       u⁹⁹ = 1.57772181044202361082345713056557245934641287021804... · 10¹⁹⁷⁷⁰

⇒ N(100,100) = 1.47857923327431013915144303218931705714497824542031... · 10¹⁹⁶⁴¹

You see, this approximation method works very good for high dimensions.
Unfortunately we have learned from String Theory that our universe has got only 11 dimensions.

Comparisons in dimension n=2

For n=2 (magic square series) we have got lots of data:
- Exact values up to order 150 by Robert Gerbicz and even more by Dirk Kinnaes
- Very good approximations for large m by Henry Bottomley
For n=2 the third member of the formula is not very much smaller than the first one. Thus we can expect an accuracy of only a few digits (depending on m) for the m1-approximation.

Method	m = 10	m = 100	m = 1000	m = 10000
Gerbicz, Kinnaes (exact)	78132541528	9.0430074 · 10²³⁶	6.5918292254 · 10³⁴²⁴	-
Bottomley (approx.)	78120036444	9.0430064 · 10²³⁶	6.5918292275 · 10³⁴²⁴	2.945158 · 10⁴⁴³³⁰
m1-approximation	78371381680	9.0466982 · 10²³⁶	6.592103 · 10³⁴²⁴	2.945170 · 10⁴⁴³³⁰

The table confirms the different methods impressively.

n=2 is the worst case for the m1-approximation. Bottomley's experimental formula works much better, but we can't apply it for other dimensions.

Magic series for cubes (n=3)

m3-approximation
By comparing exact data with their m1-approximation we can estimate the values of the third coefficients.
See text-file third-coefficients-numerators.txt.
Using these additional data we can find very good approximations of the numbers of magic cube series.

For example: N₃(100) ≈ 1.4713509428 · 10⁴³⁵ (Expected relative error < 10^-10 )

See text-file magic-cube-series.txt for the numbers of cube series up to order 150.

Overview

This chapter needs an update because Kinnaes' algorithm offers new possibilities.

Back to the Table of Contents